音乐与数学 课程笔记

临时抱佛脚。

节拍与节奏

拍子 beat

基本律动

节拍 meter

若干拍子按照一定强弱规律组合成节拍

单拍子 二拍子，三拍子
复拍子 由相同的单拍子结合而成的

素数拍只能是单拍子

拍号 time signature

表示节拍

特别提醒

$C = \frac{4}{4}$

节奏 rhythm

由音符的不同时值组合构成的模式

古巴颂乐

[..X.X...|X..X..X.] (2-3 形式)
or
[X..X..X.|..X.X...] (3-2 形式)

极大均衡原则 maximal evenness

将起拍尽可能均匀分布

16 拍节奏性包含 5 个起拍，平均间隔 $16 / 5 = 3.2$

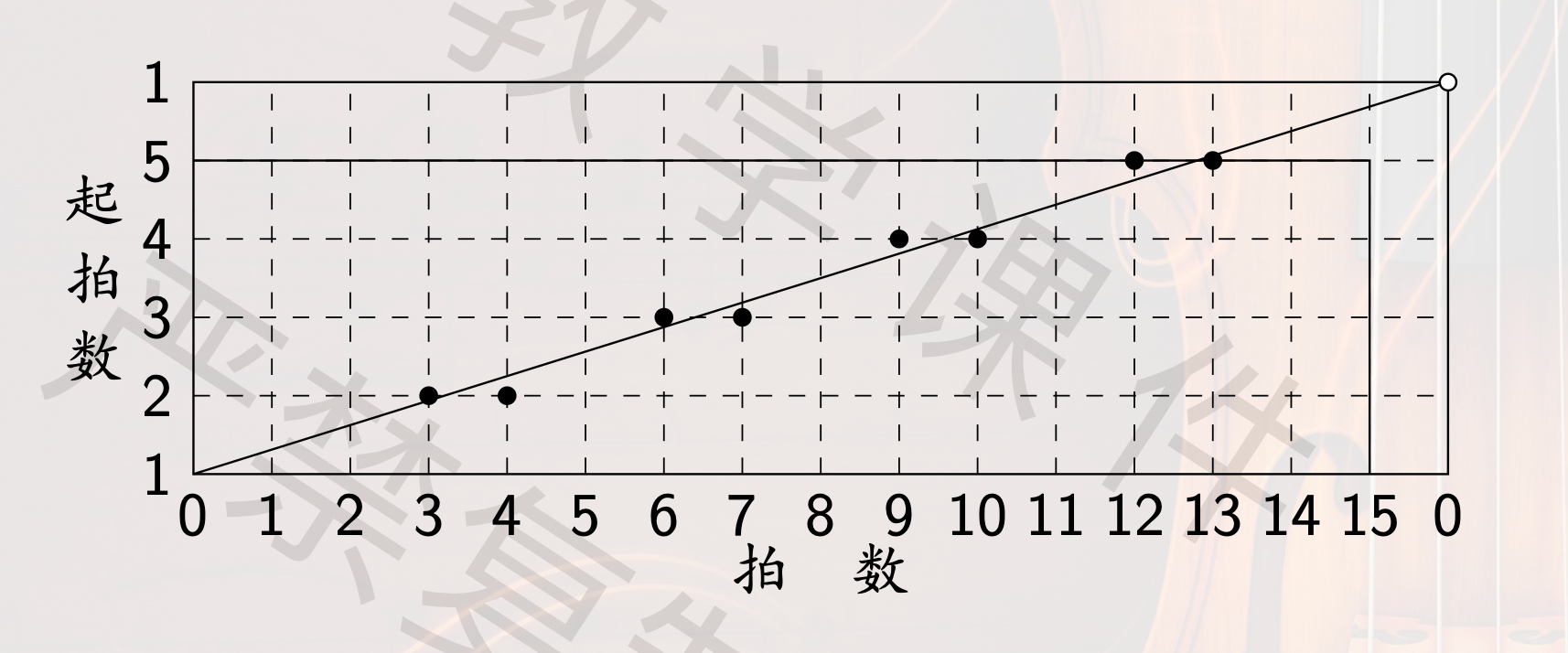
极大均衡原则

第一个起拍位于第 0 拍，可以得到 $2^{4} = 16$ 种

相位 phase

同一节奏型选取不同起点形成不同相位

节奏奇性 rythmic oddity

不包含对径的起拍对（起拍的对径点不是起拍）

古巴颂乐的节奏型具有节奏奇性

距离序列

[X..X..X.|..X.X...]
[ 3  3   4   2  4 ] 距离序列
[ 0  +   -   +  - ] 轮廓 contour

轮廓

contour[i] 表示 下一个 相对 这一个 是增加、相等还是减小

轮廓同构：B 的轮廓循环移位得到 A 的轮廓

影子节奏

拍点位置在原节奏两个拍点中间

[X..X..X.|..X.X...]
[ 3  3   4   2  4 ][ 3  3   4  ... 距离序列
[ 0  +   -   +  - ]                轮廓
..[3  3.5  3   3 3.5][3  3.5  3... 影子节奏的距离序列
  [+   -   0   +  - ]              影子节奏的轮廓

古巴颂乐和它的影子节奏轮廓同构

音乐基础知识

声波是纵波
振动频率决定音乐中的 音高（pitch）
振动幅度决定音乐中的 力度（dynamics）
- 听到声音的 响度（loudness） 是由传入空气的压力决定的
声音持续时间长度对应音乐中的 时值（duration）
振动 波形（waveform） 决定音乐中的 音色（timbre）

音乐会音高 中央 C 上方 A 定义为 400Hz

声音的物理属性

声压 - 力度

空气压力

声压水平 - 分贝

人对声音强弱感觉不是线性的，用声压水平度量

L_{p} = 20 \log_{10} \frac{p}{p_{0}}

$p_{0}$ 是 1000Hz 听觉下限阈值 $20 μ P a$ ，此时单位为分贝 dB

信息

人对不同频率的声音有着不同的听觉下限阈值

波形面面观 - 振幅包络 envelope

ADSR

振幅
|
|------/\---------------- 极大振幅
|     /  \
|    /    \
|   /      ---------
|  /                \
| /                  \
|/                    \
|------------------------- 时间
|<  A  ><D><   S   ><R>

Attack 起音
Decay 衰减
Sustain 持续
Release 释放

频谱图

描述声音的各个频率成分随时间变化的图形

泛音列

把声音的各个频率成分从低到高排列起来的序列

傅立叶级数

两种视角

把一个振动（函数）描绘成随时间变化的图形，显示 时域（time domain） 上的特性
把该振动在不同频率上的振幅描绘出来，显示 频域（frequency domain） 上的特性

打击乐器 - 噪音

固定音高 木琴、定音鼓
无固定音高 小军鼓、大镲

乐音体系

音乐中所使用的、具有固定音高的全体乐音构成的集合

音级乐音体系中的元素
音列全体音级从低到高排列
半音、全音
音名
基本音级 C D E F G A B + 变音记号 → 变化音级

特别注意

异名同音

一个音级可以有不同的音名，相同音高不同音名称为等音（enharmonic）

唱名

固定唱名法 fixed do
- do = $C$
- re = $D$
- mi = $E$
- …
首调唱名法 movable do
- 按照 mi fa 和 si do 半音，其余全音规则排列

记谱法

音符代表的时值是 相对长度，以四分音符为一拍，全音符的时值为 4 拍。

全休止符在上、二分休止符在下

高音谱号（ $G$ 谱号）
- 大圆圈位于二线，指明中央 $C$ 上方纯五度 $G_{4}$ 的位置
中音谱号（ $C$ 谱号）
- 中心位于三线，指明中央 $C$ ，即 $C_{4}$ 的位置
- 若将中心置于四线，称之为次中音谱号
低音谱号（ $F$ 谱号）
- 冒号中心位于四线，指明中央 $C$ 下方纯五度 $F_{4}$ 的位置

谱表

记有谱号的五线谱

单谱表
联合谱表
- 用 连谱号 联结起来的若干单谱表
- 大谱表 = 高音谱表 + 低音谱表

音程

两个音级之间的距离
音程中高的音称为上方音/冠音，低的音称为下方音/根音

旋律音程
- 两个音先后发声
和声音程
- 两个音同时发声

音程的名称由度数和 半音数 共同决定

度数	半音数	名称
一	0	纯一度
二	1	小二度
二	2	大二度
三	3	小三度
三	4	大三度
四	5	纯四度
四	6	增四度
五	6	减五度
五	7	纯五度
六	8	小六度
六	9	大六度
七	10	小七度
七	11	大七度
八	12	纯八度

特别注意

基本音级上的四度不全是纯四度 F-B 是增四度
基本音级上的五度不全是纯五度 B-F’ 是减五度

        （二、三、六、七）
        大音程    小音程
减音程                    增音程
            纯音程
        （一、四、五、八）

协和音程与不协和音程

协和音程
- 完全协和音程纯四度、纯五度、纯八度
- 不完全协和音程大小三度、大小六度
不协和音程
- 二度、七度、所有增减音程

毕达哥拉斯理论

频率之比越简单，音程越和谐

纯五度 $3 : 2$
纯四度 $4 : 3$
大六度 $5 : 3$
大三度 $5 : 4$
小三度 $6 : 5$
小六度 $8 : 5$
小七度 $9 : 5$
大二度 $9 : 8$
大七度 $15 : 8$
小二度 $16 : 15$
增四度 $45 : 32$ （三全音）

拍音理论

频率 $ω_{1}$ 和 $ω_{2}$ 的两个声音叠加，拍音频率

δ = | ω_{1} - ω_{2} |

不含拍音的为协和音程，含有拍音的为不协和音程

实际中，拍音频率小于 6 或者大于 120 的也算作协和音程，而 33 时最不协和

缺陷：相同音程在不同音区会发生变化

振动方程与泛音

一维振动方程

对弦上微元 $Δ x$ 作牛顿第二定律分析可得

\begin{matrix} \frac{\partial^{2} u}{\partial t^{2}} = c^{2} \frac{\partial^{2} u}{\partial x^{2}} \\ u (0, t) = u (L, t) = 0, \forall t \geq 0 \end{matrix}

其中 $c = \sqrt{\frac{T}{ρ}}$

$(2)$ 式为弦两端固定的边值条件

方程的完整解为

\begin{aligned} u (x, t) & = \sum_{n = 1}^{\infty} u_{n} (x, t) \\ = \sum_{n = 1}^{\infty} (a_{n} \cos (\frac{n π c}{L} t) + b_{n} \sin (\frac{n π}{L} x)) \\ = \sum_{n = 1}^{\infty} (\sqrt{a_{n}^{2} + b_{n}^{2}} \sin (ω_{n} t + θ_{n}) \sin (\frac{n π}{L} x)) \end{aligned}

称 $u_{n} (x, t)$ 为弦振动的第 $n$ 个振动模态

u_{n} (x, t) = \sqrt{a_{n}^{2} + b_{n}^{2}} \sin (ω_{n} t + θ_{n}) \sin (\frac{n π}{L} x)

ω_{n} = \frac{n π c}{L}

频率 $f_{n}$ 为 $u_{n} (x, t)$ 的振动频率

\begin{aligned} f_{n} = \frac{n}{2 L} c & = \frac{n}{2 L} \sqrt{\frac{T}{ρ}}, n = 1, 2, 3, \dots \\ f_{1} & = \frac{1}{2 L} \sqrt{\frac{T}{ρ}} \end{aligned}

梅森定律

弦的固有频率
- 振动频率组成的序列 ${f_{n}}$
$f_{1}$ 称为基频，相应的声音称为基音
$f_{n} (n > 1)$ 对应的声音统称为泛音
$f_{2}$ 对应第一泛音， $f_{3}$ 对应第二泛音…
泛音列
- 记基频 $f_{1} = f$ ，则固有频率序列为 $f, 2 f, 3 f, 4 f, \dots$ ，这个序列称为泛音列

波节与波腹

u_{n} (x, t) = \sqrt{a_{n}^{2} + b_{n}^{2}} \sin (ω_{n} t + θ_{n}) \sin (\frac{n π}{L} x)

振幅为

\sqrt{a_{n}^{2} + b_{n}^{2}} \sin (\frac{n π}{L} x)

令 $n π x / L = k π, k = 1, 2, 3, \dots$ ，可解得波节 $x = k L / n$ ，类似可解波腹

拨弦

拨弦给定了振动方程的另外两个边值条件：初始形状和初始速度

初始形状可以表示为一个折线函数 $ϕ (x)$ ，同时满足

ϕ (x) = u (x, 0) = \sum_{n = 1}^{\infty} a_{n} \sin (\frac{n π}{L} x)

这是折线函数作奇延拓后的正弦展开

对初始速度方程 $ψ (x)$ ，满足

\begin{aligned} ψ (x) & = {\frac{\partial u}{\partial t} |}_{t = 0} \\ = \sum_{n = 1}^{\infty} b_{n} \frac{n π c}{L} \sin (\frac{n π}{L} x) \end{aligned}

假定松手时弦静止，即 $ψ (x) \equiv 0, \forall x \in [0, L]$ ，则 $b_{n} = 0$

最终结果（在弦的中央拨弦）

u (x, t) = \sum_{n = 1}^{\infty} (- 1)^{k} \frac{8}{(2 k + 1)^{2} π^{2}} \cos (\frac{(2 k + 1) π c}{L} t) \sin (\frac{(2 k + 1) π}{L} x)

振动频率为 $(2 k + 1) c / 2 L$ ，为基频的奇数倍，即在固有频率中只出现 $f_{1}, f_{3}, f_{5}, \dots$

几何解释

在 $L / 2$ 处拨弦，弦的振动应当始终关于 $L / 2$ 对称，只有基频奇数倍的频率的振动模态波形满足此条件

管乐器

管乐器空气柱振动的边值条件与弦振动不同

振动的空气柱会超过管的端口，需要进行端口校正

声速 $v$ ，频率 $f$ ，波长 $λ$ ，有关系式

f = \frac{v}{λ}

若不计端口校正，则管的开口位置总是处于振动的波腹，闭口位置只能处于波节，这给出了边值条件。通过这两个条件可以得到管长 $L$ 与波长 $λ$ 的关系

对于开管乐器，最长的波长 $λ_{1}$ 满足 $L = λ_{1} / 2$ ，记 $f = f_{1} = v / 2 L$ 为基频，则泛音列为

f, 2 f, 3 f, 4 f, \dots

对于闭管乐器，最长的波长 $λ_{1}$ 满足 $L = λ_{1} / 4$ ，记 $f = f_{1} = v / 4 L$ 为基频，则泛音列为

f, 3 f, 5 f, 7 f, \dots

即闭管只有偶次泛音

超吹：产生泛音列中第二个频率

长笛是开管乐器，超吹产生的是高八度的音 $2 f$
单簧管是闭管乐器，超吹产生的是高十二度的音 $3 f$

律学

三分损益

假设 $宫$ 的弦长为 $3^{4} = 81$ ，从此开始，向上 $\times \frac{4}{3}$ （纯四度）得到 $徵 = 108$ ，从 $徵$ 向下 $\times \frac{2}{3}$ （纯五度）得到 $商 = 72$ ，再向上得到 $羽 = 96$ ，再向下得到 $角 = 64$

线长与频率成反比，将 $徵 = 108$ 和 $羽 = 96$ 除以 2，得到高八度的两个音级（数字表示弦长）

徵	羽	宫	商	角	徵	羽
108	96	81	72	64	54	48

假定宫音对应中央 C，由此产生五声音阶

徵	羽	宫	商	角	徵	羽
G	A	C	D	E	G	A

问题：音程 宫-角 比例不是理想大三度的整数比 $5 : 4$ ，而是 $\frac{81}{64}$

从 $角 = 64$ 继续出发，向上得到 $变宫 = \frac{256}{3} \approx 85$ ，向下得到 $变徵 = \frac{512}{9} \approx 57$ ，形成七声音阶（古音阶）

通过三分损益不停作 $\times \frac{4}{3}$ 和 $\times \frac{2}{3}$ 可以得到十二律，得到的高八度音比清宫 C’ 略高，形成 旋宫不归 问题

五度相生

假设音名 $C$ 对应频率为 $1$ ，用纯五度 $3 : 2$ 作为生律元素，不停向上 $\times \frac{3}{2}$ ，超出八度则多 $\times \frac{1}{2}$ 将其降低八度，直到产生全部十二个音名

问题：音程 C-E 比例不是理想大三度的整数比 $5 : 4$ ，与 宫-角 相同。

毕达哥拉斯音差

在得到 #E 后，继续向上构建应当得到与 C’ 等音的 #B 但是在降低一个八度后，这个音的频率是

\frac{3^{12}}{2^{19}} = \frac{531441}{524288} \approx 1.013643

这个略大于 $1$ 的数便是 毕达哥拉斯音差

\frac{3^{12}}{2^{19}} = {(\frac{3}{2})}^{12} \times {(\frac{1}{2})}^{7}

即从 $C$ 出发连续向上构建 $12$ 次纯五度（ $7$ 个半音），然后降低 $7$ 个八度（ $12$ 个半音），回到了比 $C$ 略高的位置

音乐的类型

单声音乐
- 单一曲调构成的音乐
- 例如没有伴奏的独唱、独奏、曲调作同度或八度重叠的齐唱、齐奏
多声部音乐
- 复调音乐
  - 不同声部具有各自的相对独立性，按照 对位法 结合在一起
  - 例如里切卡尔（Ricercar，无插部赋格）
- 主调音乐
  - 以一个声部为主要旋律声部，其余声部相对缺少独立性，对主要旋律声部起伴奏、烘托作用

纯律

$C = 1$
纯八度 $2 : 1$
纯五度 $3 : 2$
纯四度 $4 : 3$
大三度 $5 : 4$

由此可以得到

$C = 1$
$D = ?$
$E = \frac{5}{4}$
$F = \frac{4}{3}$
$G = \frac{3}{2}$
$A = \frac{5}{3}$
$B = ?$
$C^{'} = 2$

纯五度 $E - B$ 得到 $B = \frac{15}{8}$ ，纯五度 $G - D^{'}$ 得到 $D^{'} = \frac{9}{4}$ ，进而 $D = \frac{9}{8}$

纯率中的正三和弦 $C - E - G$ ， $F - A - C^{'}$ ， $G - B - D^{'}$ 都符合简单整数比 $4 : 5 : 6$

问题

五度音程 $D - A$ 不协和，比例 $\frac{5}{3} : \frac{9}{8} = \frac{40}{27} = \frac{80}{54} < \frac{81}{54} = 3 : 2$
有两种不同的大二度（全音）： $C - D$ ， $F - G$ ， $A - B$ 为 $9 / 8$ ，而 $D - E$ ， $G - A$ 为 $10 / 9$
谐调音差
转调问题（是由于五度音程 $D - A$ 不协和引起的）

谐调音差

从 $C$ 出发升高 $4$ 个纯五度（ $7 \times 4 = 28$ ），再降低 $2$ 个八度和 $1$ 个大三度（ $12 \times 2 + 4 = 28$ ），得到

{(\frac{3}{2})}^{4} \times {(\frac{1}{2})}^{2} \times \frac{4}{5} = \frac{81}{80}

即回到比 $C$ 略高的地方。数值 $81 / 80 = 1.0125$ 被称为 谐调音差

十二平均律

\sqrt[12]{2} \approx 1.059 \dots

音分

两个频率分别为 $f_{1}, f_{2} (f_{1} < f_{2})$ 的声音之间的音分数等于

1200 l o g_{2} (\frac{f_{2}}{f_{1}})

对于平均律，半音之间差 $100$ 音分

各种换算…

音乐会音高 $A = 440 Hz$

音乐与随机性

随机变量 $ξ$ ，取值范围 $Ω = {1, 2, \dots}$
随机事件 $ξ = k$ 的概率 $P {ξ = k}$
$ξ$ 在取值范围内所有概率列成表，称为随机变量 $ξ$ 的 概率分布
条件概率…

马尔科夫链

\begin{aligned} P {ξ_{n + 1} = k_{n + 1} | ξ_{0} = k_{0}, ξ_{1} = k_{1}, \dots, ξ_{n} = k_{n}} \\ = & P {ξ_{n + 1} = k_{n + 1} | ξ_{n} = k_{n}} \end{aligned}

移动到下一个状态 ${ξ_{n + 1} = k_{n + 1}}$ 的概率只与当前状态 ${ξ_{n} = k_{n}}$ 有关，与过去所有状态无关，称为 无记忆性

时间齐次：若马尔科夫链中所有条件概率不随时间变化，此时可以用矩阵刻画马尔科夫链的行为

转移概率

P {ξ_{t + 1} = k_{j} | ξ_{t} = k_{i}} = p_{i j}

$p_{i j}$ 构成的矩阵称为 转移概率矩阵，有性质 $\sum_{j = 1}^{n} p_{i j} = 1$ （每一行元素之和为 $1$ ）

高阶马尔科夫链：下一个状态与过去 $m$ 个状态有关，称为 $m$ 阶马尔科夫链

噪声音乐、 $1 / f$ 音乐

功率谱
- 随机序列的平均功率沿频率轴的分布
- 等于序列 自相关函数 的傅立叶变换，自相关函数反应了随机序列的 自相似性
无标度噪声
- 功率谱为常数，各频率上平均功率相等
- 白噪声 是一种无功率噪声，自相关函数除去原点为 $0$ ，任意时刻随机变量取值的涨落与前一个状态无关
  - 功率谱密度在频率 $f$ 轴上是常数，即等于 $1 / f^{0}$
  - 白色音乐
布朗噪声与棕色音乐
- 从一个音级出发，随机得到 $0, \pm 1, \pm 2, \pm 3$ 之一，表示下一个音级升高或降低的半音数（或音级数）
- 有较强的自相关性，其功率谱密度反比于频率的平方 $1 / f^{2}$
粉噪声
- $1 / f$ 噪声
- 产生方式
  - 若干骰子掷给出初始状态
  - 之后第 $n$ 次掷骰子按照 $n$ 到 $n + 1$ 的二进制改变的比特数 $m$ 掷前 $m$ 个骰子，其余保持不变

白噪声（假设功率谱密度为 $1$ ）在固定带宽 $Δ$ 的任意频段上平均功率等于常数

\int_{F}^{F + Δ} 1 d f = f |_{F}^{F + Δ} = Δ

粉噪声在任意八度频段上平均功率等于常数

\int_{F}^{2 F} \frac{1}{f} d f = {\ln f |}_{F}^{2 F} = \ln 2

调式、音阶与和弦

调式

若干音级围绕某个有 稳定感 的中心音级，按照一定音程关系组织起来的乐音体系
中心音级为主音

自然大调

由两个相同的四声音阶结合而成，每个四声音阶的四个音级之间分别构成 大二度大二度小二度 音程
两个四声音阶之间相隔大二度

从主音开始全全半全全全半

I	II	III	IV	V	VI	VII
主音	上主音	中音	下属音	属音	下中音	导音

小调

自然小调

由两个不同的四声音阶结合而成，每个四声音阶的四个音级之间分别构成 大二度小二度大二度 和 小二度大二度大二度 音程
两个四声音阶之间相隔大二度

从主音开始全半全全半全全

和声小调：将自然小调的第 VII 级音导音升高半音
旋律小调：将和声小调第第 VI 级音也升高半音，以去除和声小调 VI-VII 之间的增二度
- 旋律小调下行时恢复上行时升高的 VI 和 VII 级音，与自然小调的下行音阶相同

特别提醒

和声小调和旋律小调的升与还原不在调号中体现，只标临时升降号

升号调

按照五度循环规律依次考虑以 C, G, D, A, E, B, #F, #C 为主音的自然大调音阶，每次多升一个音级

主音	升号数	升号音级
C	0
G	1	#F
D	2	#F, #C
A	3	#F, #C, #G
E	4	#F, #C, #G, #D
B	5	#F, #C, #G, #D, #A
#F	6	#F, #C, #G, #D, #A, #E
#C	7	#F, #C, #G, #D, #A, #E, #B

此时已经升满七个音，再升没有意义

降号调

对称考虑反方向五度循环，以 C, F, ♭B, ♭E, ♭A, ♭D, ♭G, ♭C 为主音的大调音阶，每次多降一个音级

主音	降号数	降号音级
C	0
F	1	♭B
♭B	2	♭B, ♭E
♭E	3	♭B, ♭E, ♭A
♭A	4	♭B, ♭E, ♭A, ♭D
♭D	5	♭B, ♭E, ♭A, ♭D, ♭G
♭G	6	♭B, ♭E, ♭A, ♭D, ♭G, ♭C
♭C	7	♭B, ♭E, ♭A, ♭D, ♭G, ♭C, ♭F

等音调

十五个自然大调中存在三对等音调（在十二平均律键盘乐器上，音阶在键盘的位置完全一样）

B 和 ♭C
#F 和 ♭G
#C 和 ♭D

调式之间的关系

关系大小调
- 调号相同的一对大小调
平行大小调
- 主音相同的一对大小调
近关系调
- 每个调式有 5 个近关系调
- X 大调属音大调属音大调的关系小调
  关系小调
  下属音大调下属音大调的关系小调
- x 小调属音小调属音小调的关系大调
  关系大调
  下属音小调下属音小调的关系大调

和弦

三个或者三个以上不同音高的乐音按照一定的音程关系结合传统和弦按照 三度叠置原则 构建

三和弦

按照音程排列，最下面的称为根音
中间的音与根音成三度关系，称为三音
最上面的音与根音成五度关系，称为五音或者冠音

按照两个三度的类型可以构成四种三和弦

下方大三 + 上方小三 = 大三和弦
下方小三 + 上方大三 = 小三和弦
下方大三 + 上方大三 = 增三和弦
下方小三 + 上方小三 = 减三和弦

七和弦

在三和弦上再叠加一个七度音，命名按照 三和弦类型 + 七度类型

三度结构	命名结构	名称	简称
小三小三小三	减三和弦减七度	减减七和弦	减七和弦
小三小三大三	减三和弦小七度	减小七和弦	半减七和弦
小三大三小三	小三和弦小七度	小小七和弦	小七和弦
小三大三大三	小三和弦大七度	小大七和弦
大三小三小三	大三和弦小七度	大小七和弦	属七和弦
大三小三大三	大三和弦大七度	大大七和弦	大七和弦
大三大三小三	增三和弦大七度	增大七和弦

为什么没有增增七和弦？

增七度半音数与纯八度一致，听感上与增三和弦一致

七和弦至少包括一个不协和的七度音程，所以都是不协和和弦
实际作品中大小七和弦（属七和弦）、大七和弦、小七和弦、减七和弦、半减七和弦较为常见、其他七和弦较少出现
重升号和重降号的使用是为了满足三度叠置原则

和弦的转位

三和弦
- 第一转位（六和弦），此时低音与高音相差六度
- 第二转位（四六和弦），此时低音与中音、高音分别相差四度和六度
七和弦
- 第一转位（五六和弦）
- 第二转位（三四和弦）
- 第三转位（二和弦）

和弦标记

用罗马数字表示和弦根音在调式音阶中的级数
- 根音到三音为大三度：大写
- 根音到三音为小三度：小写
用上标 $^{\circ}$ 和 $^{+}$ 分别表示减三和弦和增三和弦，大、小三和弦不加上标
用下标 $_{6}$ 和 $_{\begin{matrix} 6 \\ 4 \end{matrix}}$ 分别表示三和弦的第一转位和第二转位

近关系调的定义

给定自然调式 X，另一个调式 Y 是 X 的近关系调，如果调式 Y 的主和弦是 X 各级大、小三和弦中的一个

和弦的功能

正和弦
- 以主音、下属音、属音构成的和弦
- 分别称为主和弦、下属和弦、属和弦
- 主和弦 I：稳定、结束、完成，开始处往往也用主和弦，强调音乐的调性特征
- 属和弦 V：不稳定，与主和弦形成对比，进行到一半、尚未结束的感觉
- 下属和弦 IV：连接和过渡作用，从主和弦出发，或者连接到属和弦

和声进行

一定和声范围内的和弦连接
正和弦的连接进行
1. 正格进行 I - V - I
2. 变格进行 I - IV - I
3. 复式进行 I - IV - V - I

大调的和弦进行

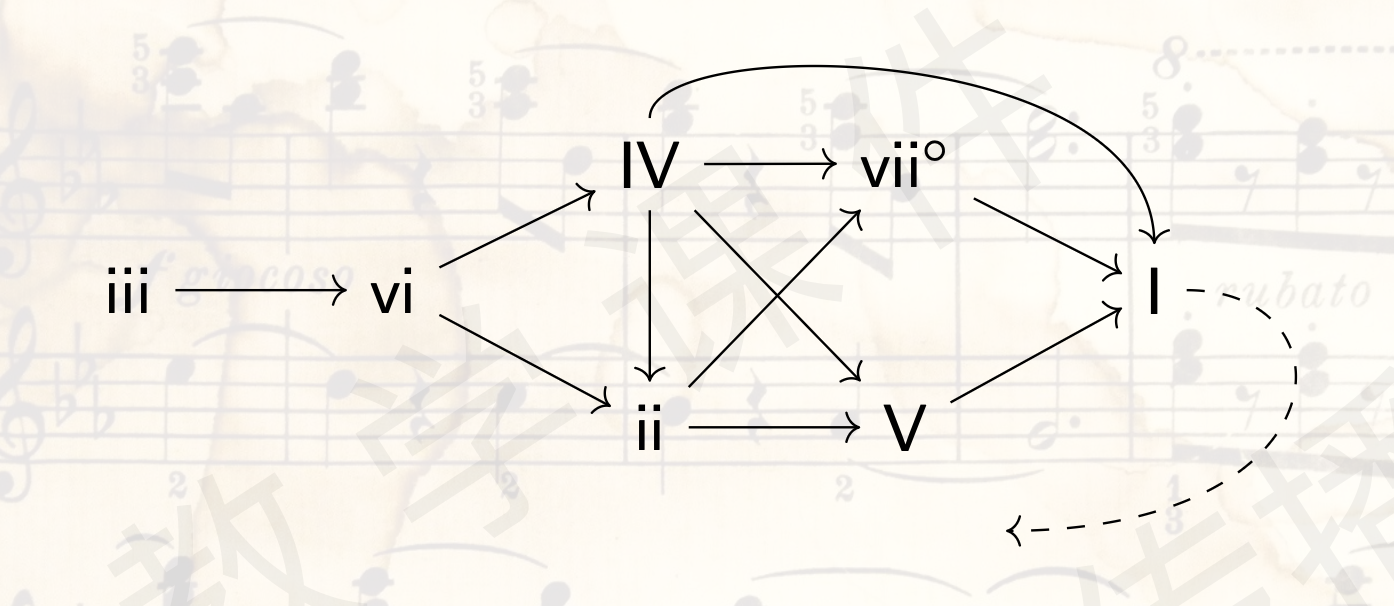
虚线表示从主和弦 I 开始可以到达任何和弦

对于小调式，只需改变图中各级和弦的属性

解决

从不协和的和弦出发，连接到协和和弦或者较为协和的和弦，这样的和弦进行

在调性音乐中，所有和弦进行最终都要解决到主和弦 I

旋律与对称

移调
- 严格移调：把一段旋律中每个音级升高或降低相同的半音数
- 调性移调：适当调整半音数，使得移调后的各个音级仍然在调式音阶中
逆行
- 按照相反次序从尾到头重复
倒影
- 将旋律中的上升音程用相同半音数的下降音程代替，将下降音程用相同半音数的上升音程代替
- 选取不同的水平直线做对称轴得到不同的倒影
- 严格倒影…

乐音体系的数字化

分类、关系

集合 $S$ 上的一个二元关系是 $S$ 中元素 有序对 构成的集合

S \times S = {(x, y) | x, y \in S}

中的一个子集合 $R \subset S \times S$

对 $\forall a, b \in S$ ，称 $a$ 与 $b$ 有关系，当且仅当 $(a, b) \in R$ ，简记作

a ≺ b

关系的三种性质
- 自反性 $a ≺ a, \forall a \in S$
- 对称性 $a ≺ b \Leftrightarrow b ≺ a, \forall a, b \in S$
- 传递性 $a ≺ b and b ≺ c \Rightarrow a ≺ c, \forall a, b, c \in S$

若集合 $S$ 上的一个关系同时具备上述三个性质，称其为 $S$ 上的一个 等价关系

八度关系

设乐音体系是由 8 个八度和 $C_{8}$ 构成的，等音的音级视为相等

M = {C_{0}, \dots, B_{0}, C_{1}, \dots, B_{1}, \dots, C_{7}, \dots, B_{7}, C_{8}}

八度关系是乐音体系 $M$ 上的一个等价关系

等价类

给定集合 $S$ 上的一个等价关系，对任意两个元素 $a, b \in S$ ，如果 $a$ 与 $b$ 有关系，则称 $a$ 与 $b$ 等价，记为 $a \sim b$ ，定义 $S$ 的子集合

\overset{―}{a} = {b \in S | b \sim a}

为包含 $a$ 的等价类

等价类的性质
- 不重：任意两个等价类或者相等，或者互不相交
- 不漏：集合 $S$ 可以表示成若干互不相交的等价类之并
- 即：给定 $S$ 上一个等价关系，得到集合中全部元素的一个分类

音类、音类空间

$M$ 按照八度关系形成的等价类
八度关系把所有音级分成 12 个音类
12 个音类构成的集合 $PC$ 称作音类空间

音乐变换群

群

对非空集合 $G$ ，存在一个代数运算 $*$ ，满足

结合律： $(a * b) * c = a * (b * c), \forall a, b, c \in G$
$G$ 中存在 单位元 $e$ ，满足 $a * e = e * a = a, \forall a \in G$
对任意 $a \in G$ ，存在 逆元素 $b \in G$ ，使得 $a * b = b * a = e$

称代数结构 $(G, *)$ 是一个群，通常将运算称为乘法，逆元素记为 $a^{- 1}$ ， $G$ 中元素个数称为这个群的阶，记为 $| G |$

特别提醒

群中运算不一定满足交换律，满足交换律的群称作 交换群 或 Abel 群

由一个元素生成的群称为 循环群，这个元素称为 生成元

暂时不能给你明确的答复

后面没学懂，已放弃

这需要你自己衡量！

~~我觉得是这是数学与数学，而不是音乐与数学~~

文件历史

content: quit warning for music'n'math b2cd9c4

2025 年 11 月 3 日 13:14djdjz7

chore: created 'notes' section b7da2e6

2025 年 9 月 9 日 14:06djdjz7

chore: bump vite to 7.1.3 & fmt 27b6c28

2025 年 8 月 30 日 06:16djdjz7

feat: backport tags support cb2b6c5

2025 年 6 月 24 日 02:37djdjz7

blog: music and math part ii b79830a

2025 年 6 月 3 日 11:35djdjz7

blog: music and math part i 50f2957

2025 年 6 月 1 日 16:05djdjz7

X 大调	属音大调	属音大调的关系小调
	关系小调
	下属音大调	下属音大调的关系小调

x 小调	属音小调	属音小调的关系大调
	关系大调
	下属音小调	下属音小调的关系大调

博客

笔记

生活

文章

音乐与数学 课程笔记

# 节拍与节奏

# 拍子 beat

# 节拍 meter

# 拍号 time signature

# 节奏 rhythm

# 极大均衡原则 maximal evenness

# 相位 phase

# 节奏奇性 rythmic oddity

# 距离序列

# 轮廓

# 影子节奏

# 音乐基础知识

# 声音的物理属性

# 声压 - 力度

# 声压水平 - 分贝

# 波形面面观 - 振幅包络 envelope

# 频谱图

# 泛音列

# 傅立叶级数

# 打击乐器 - 噪音

# 乐音体系

# 异名同音

# 唱名

# 记谱法

# 谱表

# 音程

# 协和音程与不协和音程

# 毕达哥拉斯理论

# 拍音理论

# 振动方程与泛音

# 一维振动方程

# 梅森定律

# 波节与波腹

# 拨弦

# 最终结果（在弦的中央拨弦）

# 几何解释

# 管乐器

# 律学

# 三分损益

# 五度相生

# 毕达哥拉斯音差

# 音乐的类型

# 纯律

# 谐调音差

# 十二平均律

# 音分

# 音乐与随机性

# 马尔科夫链

# 噪声音乐、1/f 音乐

# 调式、音阶与和弦

# 调式

# 自然大调

# 小调

# 升号调

# 降号调

# 等音调

# 调式之间的关系

# 和弦

# 三和弦

# 七和弦

# 和弦的转位

# 和弦标记

# 近关系调的定义

# 和弦的功能

# 和声进行

# 旋律与对称

# 乐音体系的数字化

# 分类、关系

# 八度关系

# 等价类

# 音类、音类空间

# 音乐变换群

# 群

文件历史

音乐与数学课程笔记

节拍与节奏

拍子 beat

节拍 meter

拍号 time signature

节奏 rhythm

极大均衡原则 maximal evenness

相位 phase

节奏奇性 rythmic oddity

距离序列

轮廓

影子节奏

音乐基础知识

声音的物理属性

声压 - 力度

声压水平 - 分贝

波形面面观 - 振幅包络 envelope

频谱图

泛音列

傅立叶级数

打击乐器 - 噪音

乐音体系

异名同音

唱名

记谱法

谱表

音程

协和音程与不协和音程

毕达哥拉斯理论

拍音理论

振动方程与泛音

一维振动方程

梅森定律

波节与波腹

拨弦

最终结果（在弦的中央拨弦）

几何解释

管乐器

律学

三分损益

五度相生

毕达哥拉斯音差

音乐的类型

纯律

谐调音差

十二平均律

音分

音乐与随机性

马尔科夫链

噪声音乐、 $1 / f$ 音乐

调式、音阶与和弦

调式

自然大调

小调

升号调

降号调

等音调

调式之间的关系

和弦

三和弦

七和弦

和弦的转位

和弦标记

近关系调的定义

和弦的功能

和声进行

旋律与对称

乐音体系的数字化

分类、关系

八度关系

等价类

音类、音类空间

音乐变换群

群