半导体器件原理 1.5 Derivation of the Ideal PN Junction Diode Equation

About carrier statistics with respect to locations, external voltages, and the diffusion current with applied voltage.

# Carrier Statistics with Respect to Locations

• In a P+/N junction:
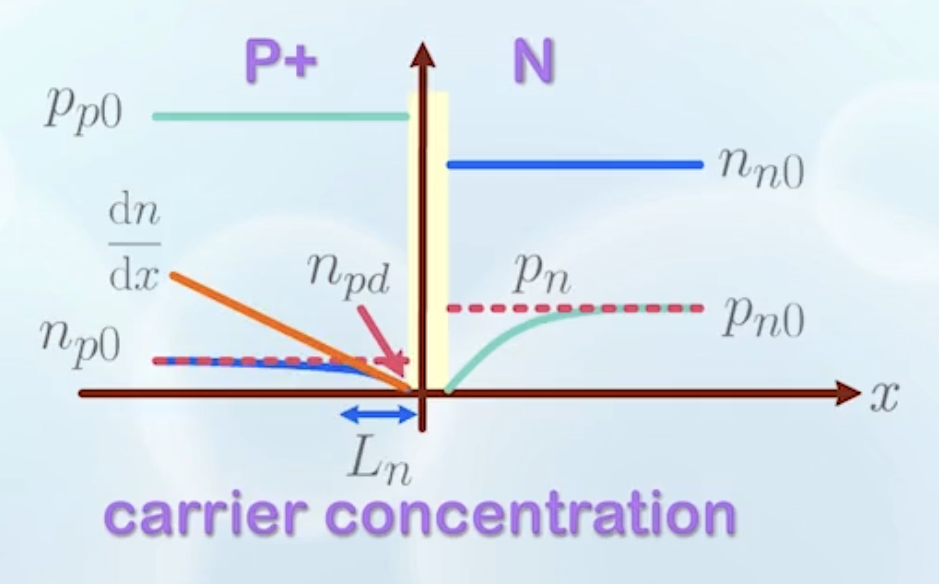
  • Carrier concentration
    • $p_{p0}\cong N_A$
    • $n_{p0}\cong n_i^2/N_A$
    • $n_{n0}\cong N_D$
    • $p_{n0}\cong n_i^2/N_D$
    • Denotations: ${\text{CarrierType}}_{\text{Region}}$, and 0 means thermal equilibrium
    • We draw the graph in log scale as carrier concentration varies a lot
  • $p_{p0}>n_{n0}$ because of heavier doping on the P side
• Carrier concentration in the depletion region is not a constant, but varies with location
  • It is difficult to calculate, so we simply ignore it, assuming it is very small compared to the neutral regions

# Carrier Motion at Thermal Equilibrium

• No net current flow at thermal equilibrium, but carriers are not stationary
• In the conduction band
  • On the N side, higher electron concentration pushes electrons to diffuse to the P side
  • Some of the electrons are driven back by drift
  • There are many electrons on the N side, but most with energy lower than $E_{Cp0}$ ($E_C$ of the P side at thermal equilibrium). These electrons cannot move to the P side
  • Electrons that can move freely across the two sides are those with energy higher than $E_{Cp0}$
  • On the P side, concentration of these high-energy electrons are $n_{p0}$
  • On the N side, concentration of electrons is governed by the Fermi-Dirac distribution, where $E_{Cp0}-E_F$ is identical to that of the P side, so the concentration is also $n_{p0}$

# Fermi-Level Under External Voltage

• The PN junction symbol
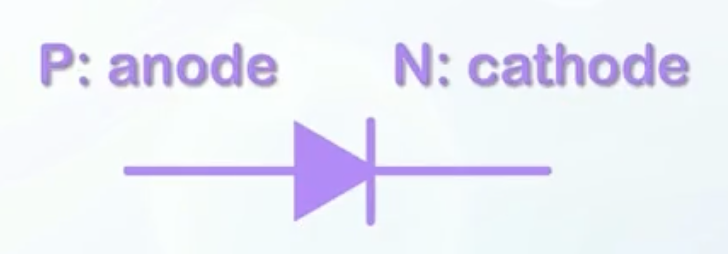
• Positive Bias/Forward Bias: Positive voltage $V_A$ on the P side with respect to the N side
• Negative Bias/Reverse Bias: Negative voltage $V_A$ on the P side with respect to the N side
• At reverse bias, alignment of the Fermi levels on the two sides is broken
  • Fermi level on the P side is raised by $q|V_A|$ with respect to the N side
  • Fermi level is the same across the neutral regions, but there is a discontinuity across the depletion region
  • In the depletion region, there are externally injected carriers, so the equilibrium cannot be assumed. Simple Fermi-Dirac distribution with one Fermi level does not apply
  • Must be handled with some advanced concepts of quasi-Fermi levels
  • For now, we will ignore the depletion region and focus on the neutral regions

# Energy Band Bending Under Reverse Bias

• When a reverse bias is applied, we need to find the new barrier height and the new depletion region width
• For the barrier height:
  • At thermal equilibrium, the barrier height is $q{V}_{bi}$
  • Under reverse bias, the barrier height is raised by $q|V_A|$
  • New barrier height: $V_{Bh}=q(V_{bi}-V_A)$ as $V_A$ is negative

    Why negative?

    $V_A$ is the potential of the P side with respect to the N side, so it is negative under reverse bias

• For the depletion region width:
  • Charge neutrality still holds$$N_A{x}_p=N_D{x}_n$$
  • The second equation becomes$$V_{Bh}=V_{bi}-V_A=\frac{q{N}_A{x}_p^2}{2{\epsilon }_{\text{Si}}}+\frac{q{N}_D{x}_n^2}{2{\epsilon }_{\text{Si}}}$$
  • Solving the two equations, we get$$x_d=\sqrt{\frac{2{\epsilon }_{\text{Si}}(V_{bi}-V_A)}{q}(\frac{1}{N_A}+\frac{1}{N_D})}$$
  • Assuming $N_A\gg N_D$ (P+/N junction), we have$$x_d\approx \sqrt{\frac{2{\epsilon }_{\text{Si}}(V_{bi}-V_A)}{q{N}_D}}$$

# Carrier Concentration at Reverse Bias

• When an electron enters the edge of the depletion region from the P side, it moves to the N side due to the slope in the band diagram (caused mainly by drift)
  • Electron concentration at the edge of the depletion region on the P side is lower
  • More electrons from the rest of the P side diffuse to the edge of the depletion region
• When we draw the graph of carrier concentration
  • The concentration on the P side becomes lower as $x$ moves to the depletion region
  • The concentration on the N side remains the same ($n_{n0}$) as the concentration is much higher than that caused by the few electrons coming from the P side
  • Similarly for holes, the concentration on the N side becomes lower as $x$ moves to the depletion region, while the concentration on the P side remains the same ($p_{p0}$)

# Diffusion Current Under Reverse Bias

• Current calculation is achieved by counting the number of electrons crossing a particular location per unit time
• It is much easier to do so at locations with lower carrier concentration
• For electrons, we calculate the current on the P side near the edge of the depletion region
  • The driving force is mainly diffusion
  • Current density for electrons (current per unit area):$$J_{n,\text{diff}}=q{D}_n\frac{\mathrm{d}n}{\mathrm{d}x}$$where $D_n$ is the diffusion coefficient of electrons, indicating how mobile electrons are in the medium
    • When $\mathrm{d}n/\mathrm{d}x$ is large, it means carrier concentration differs a lot, so more carriers are moving across
  • The corresponding current for holes is$$J_{p,\text{diff}}=-q{D}_p\frac{\mathrm{d}p}{\mathrm{d}x}$$where $D_p$ is the diffusion coefficient of holes
    • The negative sign is because holes move in the opposite direction to electrons
• In the graph, $\mathrm{d}n/\mathrm{d}x$ is the slop of electron concentration on the P side near the edge of the depletion region (this marks a straight line)
  • $n_{pd}$: electron concentration at the edge of the depletion region on the P side. It is not a constant, and varies with the applied voltage $V_A$
  • $L_n$: the distance the straight line intersects the $n_{p0}$ line. It represents the average distance an electron can diffuse before recombining. We can assume it is a known constant at this stage.
  • With these two notations, we have$$\frac{\mathrm{d}n}{\mathrm{d}x}=\frac{n_{pd}-n_{p0}}{L_n}$$and$$J_{n,\text{diff}}=q{D}_n\frac{n_{pd}-n_{p0}}{L_n}$$In this equation, all are known constants except $n_{pd}$

# Reverse Bias Current of a PN Junction

• A few more assumptions:
  • The carrier statistics in the neutral N region is not affected by the bias voltage, as the number of electrons added is very small compared to the number of electrons already there
  • The depletion region is very small compared to the neutral regions, so we can ignore its thickness
• With these assumptions, $n_{pd}$ equals to the carrier concentration in the neutral N region with energy higher than $E_{Cp}$
  • This is because concentration cannot change abruptly from P side to N side, as we’ve ignored the depletion region thickness
  • Calculate carrier concentration with Fermi-Dirac distribution$$n_{pd}=n_{p0}{e}^{-\frac{E_{Cp}-E_{Cp0}}{kT}}=n_{p0}{e}^{-\frac{q|V_A|}{kT}}=n_{p0}{e}^{\frac{q{V}_A}{kT}}$$
• Finally,$$\begin{array}{rl}{J}_{n,\text{diff}}=& q{D}_n\frac{n_{pd}-n_{p0}}{L_n}\\ =& q{D}_n\frac{n_{p0}}{L_n}(e^{\frac{q{V}_A}{kT}}-1)\end{array}$$
• The same for holes:$$\begin{array}{rl}{J}_{p,\text{diff}}=& -q{D}_p\frac{p_{n0}-p_{nd}}{L_p}\\ =& q{D}_p\frac{p_{n0}}{L_p}(e^{\frac{q{V}_A}{kT}}-1)\end{array}$$
• Combine the two:$$\begin{array}{rl}J=& J_{n,\text{diff}}+J_{p,\text{diff}}\\ =& q(D_n\frac{n_{p0}}{L_n}+D_p\frac{p_{n0}}{L_p})(e^{\frac{q{V}_A}{kT}}-1)\end{array}$$

# Conditions Under Forward Bias…

• Everything is the same as reverse bias, except that $V_A$ is now positive
• When $V_A>V_{bi}$, the depletion region disappears, and the PN junction becomes a resistor, all voltage drops across the neutral regions
• We can denote$$I_0=q(D_n\frac{n_{p0}}{L_n}+D_p\frac{p_{n0}}{L_p})$$which is a constant for a particular PN junction once the doping concentration is known
• The final equation is$$I_D=I_0(e^{\frac{q{V}_A}{kT}}-1)$$

文件历史