半导体器件原理 1.8 PN Junction Switching and Model

About the charge storage effects, PN junction diode models, and parameter extraction.

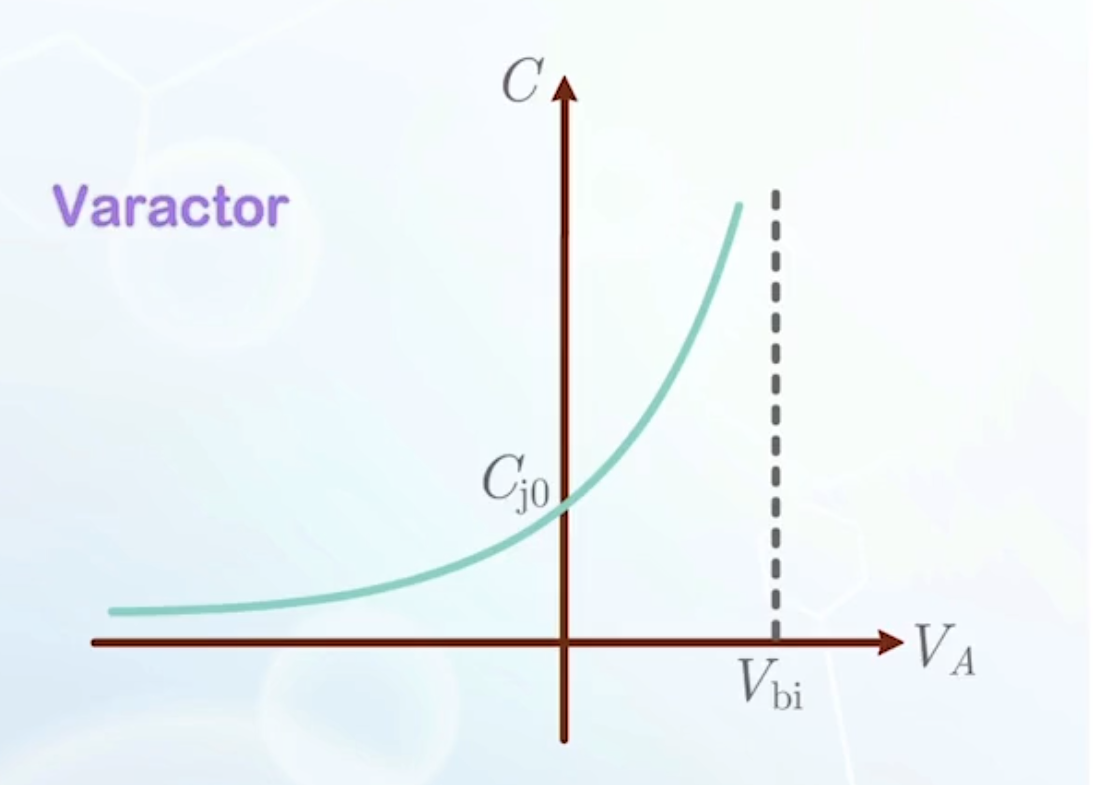
# Reverse Bias Junction Capacitance

• When switching a diode with time varying voltage, response may be delayed
  • Charges need to be accumulated to reach steady state
  • The delay can be modeled as a capacitance within the diode
• Under reverse bias, the diode can be modeled as an insulator sandwiched between two conductors, or a parallel-plate capacitor
  • The depletion region is the insulator
  • The P and N regions are the conductors
  • Its capacitance is denoted as $C_j$
  • $$C_j=\frac{{\epsilon }_{\text{Si}}A}{W_d}$$where $A$ is the cross-sectional area of the junction, and $W_d$ is the width of the depletion region.
  • We normalize it with respect to area so we can drop $A$
  • Substituting $W_d$ from previous section, we have$C_{j0}$ is bias voltage independent, representing the junction capacitance at equilibrium (zero bias).
  • The function shows that
    • Lower doping concentration leads to lower junction capacitance, due to wider depletion region
    • Capacitance of a diode can be changed by applying different voltages, making it a varactor (variable capacitor), which can select a signal at a specific frequency, but rejecting others.
    • 

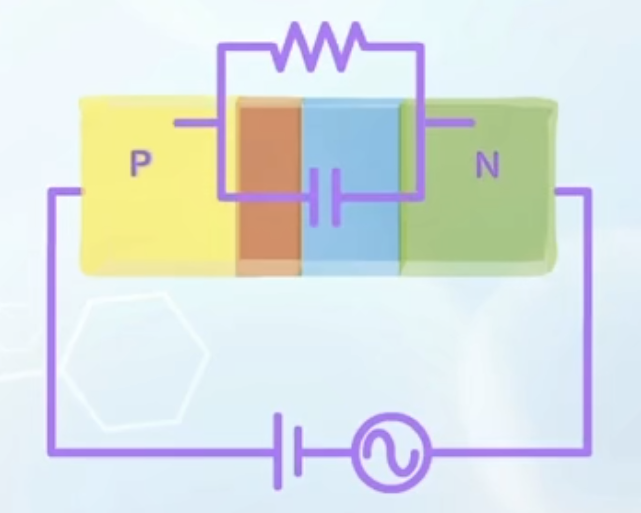
# Forward Bias Diffusion Capacitance

• Under forward bias, a current conduction path is established
  • The parallel-plate capacitor model is no longer valid
  • The diode can be modeled as a resistor in parallel with a capacitor
  • 
• For non-linear capacitors (as the case here), capacitance is defined as$$C=\frac{\mathrm{d}Q}{\mathrm{d}V}$$where $Q$ is the charge stored in the diode, and $V$ is the applied voltage.
• A PN junction under forward bias stores two kinds of charge
  • The charges in the depletion region, which has already been modeled as $C_j$ in the previous section
  • The charges of excess minority carriers injected from the opposite sides, temporarily stored before leaving (small under reverse bias, so we ignored it)
  • 
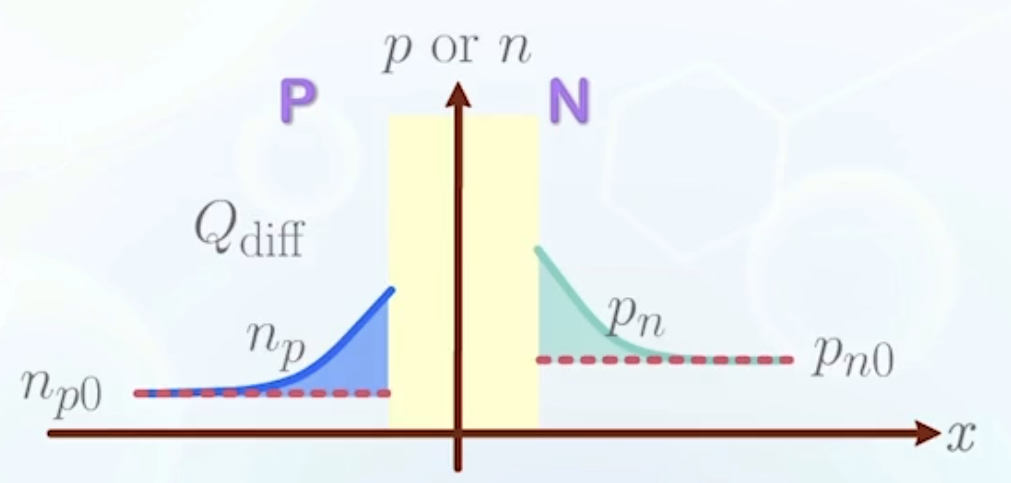
  • Carrier concentration at thermal equilibrium is not counted as stored charge since the system is electrically neutral
  • The excess minority carrier charge (diffusion charge) in P side is$$Q_{\text{diff},n}=\frac{1}{2}q(n_{pd}-n_{p0})L_n$$which is the size of the shaded area in the graph approximated as a triangle
    • Assuming injected carriers $\gg$ equilibrium carriers, we can drop $n_{p0}$
  • Adding the contribution from N side, we have the total diffusion charge$$Q_{\text{diff}}=\frac{q}{2}(L_n{n}_{p0}+L_p{p}_{n0})e^{\frac{q{V}_A}{kT}}$$
  • Differentiating it with respect to $V_A$, we have the diffusion capacitance$$C_{\text{diff}}=\frac{\mathrm{d}{Q}_{\text{diff}}}{\mathrm{d}{V}_A}=\frac{q^2}{2kT}(L_n{n}_{p0}+L_p{p}_{n0})e^{\frac{q{V}_A}{kT}}$$Or simplified as$$C_{\text{diff}}=\frac{q{Q}_{\text{diff}}}{kT}=\frac{Q_{\text{diff}}}{V_{\text{th}}}$$where $V_{\text{th}}=\frac{kT}{q}$ is the thermal voltage

# Large Signal PN Junction Model

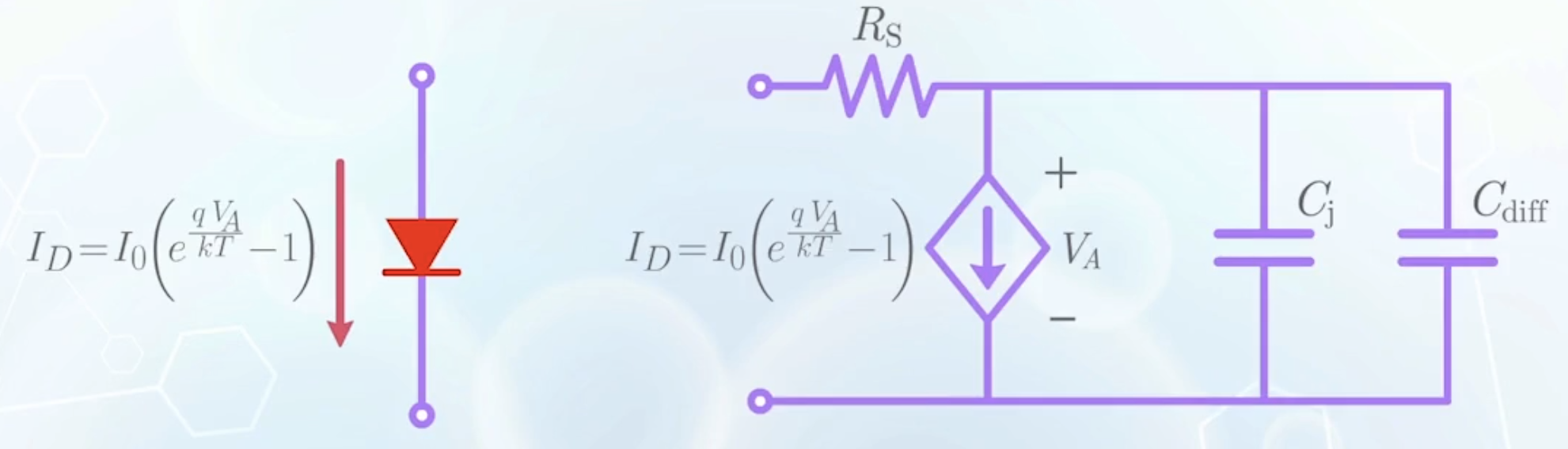
• The ideal PN junction current-voltage relationship is$$I_D=I_0(e^{\frac{q{V}_A}{kT}}-1)$$which can be represented as a voltage-controlled current source
• The neutral regions can be represented as resistor $R_S$
• To account for the charge storage effects, we add two capacitors in parallel
  • $C_j$ for junction capacitance
  • $C_{\text{diff}}$ for diffusion capacitance
  • $C_j$ dominates under reverse bias, while $C_{\text{diff}}$ dominates under forward bias, so we may only need to calculate one of them depending on the bias condition

# Small Signal PN Junction Model

When PN junction can only be operated over a small region around a bias voltage $V_b$

• The $I-V$ relationship can be approximated as the tangent of curve at that bias point
• The voltage-controlled source can be replaced with a resistor whose conductance is $G=g_d(V_b)$
• $g_d$ can be obtained by differentiating ideal diode equation with respect to voltage
• All other components ($R_S$, $C_j$, $C_{\text{diff}}$) are evaluated at $V_b$ and becomes a fixed value

# PN Junction Diode Parameter Extraction

A sample data sheet provided by diode manufacturer:

CHARACTERISTICS
$T_j=25{}^{\circ }\text{C}$ unless otherwise specified$

These values are mesured instead of calculated, and the process is called parameter extraction.

It is the process to find the values of these unknown parameters so that the values predicted by the model give the best fit to the experimental data

• $I_0$ can be read from the reverse saturation current in the log scale graph
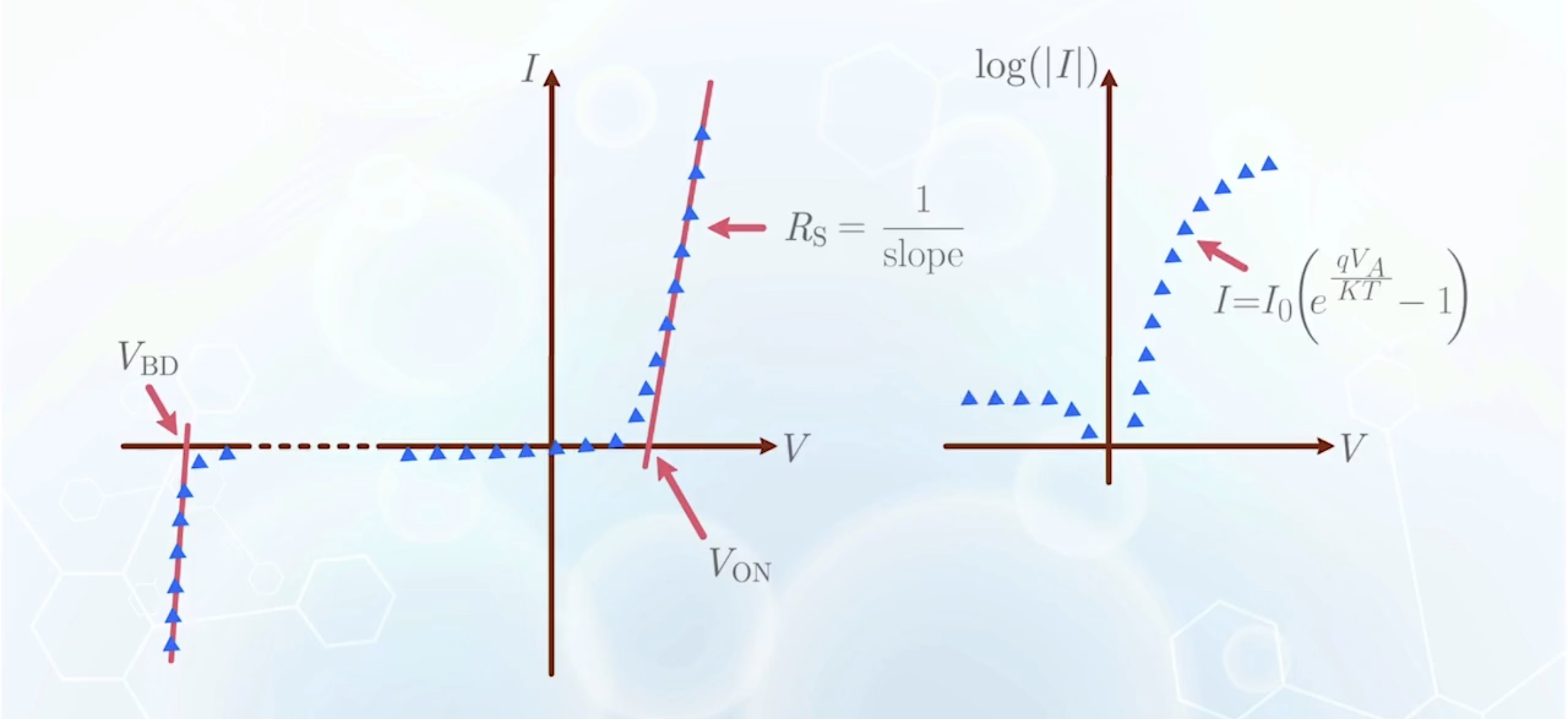
• In the forward bias region, before the diode fully turns on, the ideal diode equation may not match the experimental data, due to non-ideal effects
  • The ideality factor $n$ is introduced to account for these effects
  • The modified ideal diode equation is$$I_D=I_0(e^{\frac{q{V}_A}{\mathit{n}kT}}-1)$$
  • For an ideal diode, $n=1$, while for a real diode, $n$ is typically between 1 and 2

文件历史