半导体器件原理 2.5 Classical MOSFET Turn-on Current

About how to calculate the current of a MOSFET when it is turned on, based on the classical pinchoff model, the channel length modulation effect, and some discussions about the inconsistencies and limitations of the model.

# Charge and Velocity of Channel Carriers

MOSFET is basically a switch controlled by gate. When , electrons from the source cannot enter the channel, and no current flows. When , electrons from the source can enter the channel, and a conduction path is formed. A current will flow if a positive $V_{\text{G}}$ is applied (NMOSFET).

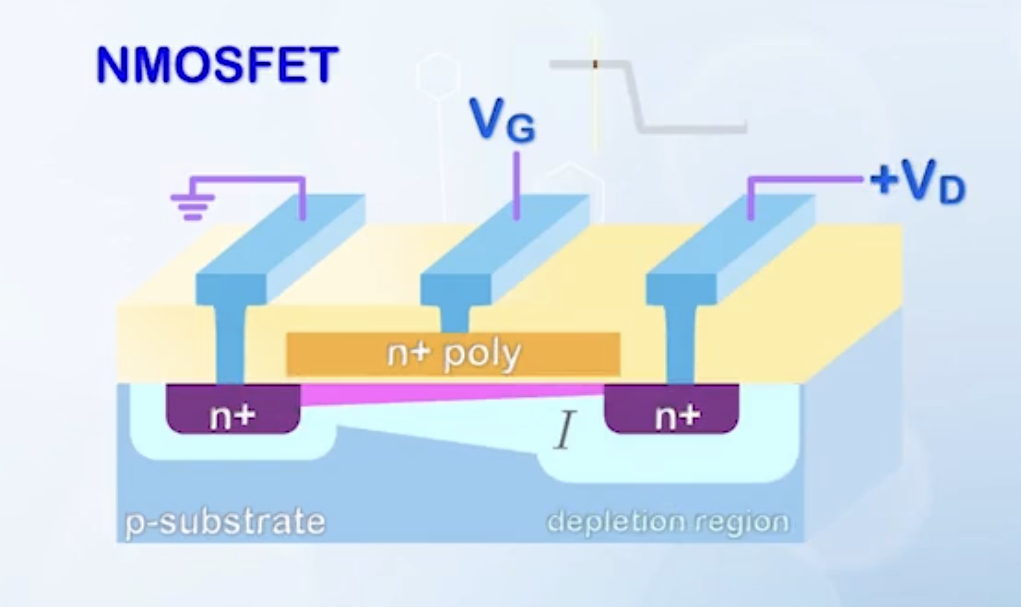
Assume source and substrate are grounded

• As a switch, $I_{\text{D}}$ is mostly assumed to be $0$ when
• When , inversion electrons form in the channel, and electrons will be attracted from the source to drain by the positive $V_{\text{D}}$
  • The electric field is the main driving force, and the current is mainly drift current
  • The current depends on the number of charge available, and the velocity of these charges
  • The current at any location $y$ is$$I(y)=Q(y)v(y)$$where $Q(y)$ is the amount of charge at location $y$
  • Defining $y$ as the coordinate from the source to drain
  • There is no accumulation or removal of charges, the current flows remains constant along the channel
    • The region with more charges will have lower velocity, and vice versa
  • Starting from a small $V_{\text{D}}$ close to $0$
    • For a MOSFET with channel length $L$ and width $W$, total charge under the gate is$$C_{ox}WL(V_{\text{G}}-V_{\text{T}})$$
    • The charge per unit length is the above divided by $L$$$Q(y)=C_{ox}W(V_{\text{G}}-V_{\text{T}})$$
  • When $V_{\text{D}}$ increases, the voltage across the gate capacitor near the drain will be reduced to $V_{\text{G}}-V_{\text{D}}$, so the charge per unit length near the drain becomes$$Q(y)=C_{ox}W(V_{\text{G}}-V_{\text{T}}-V_{\text{D}})$$which means, the charge near the drain is less than that near the source
    • The voltage in the channel somewhere between source and drain is $V(y)$, so the charge per unit length at location $y$ is$$Q(y)=C_{ox}W(V_{\text{G}}-V_{\text{T}}-V(y))$$$V_{\text{T}}$ should be a function of $y$, as increasing $V(y)$ is similar to decreasing $V_{\text{D}}$, but the effect is ignored for now
  • The velocity of electrons are usually assumed to be proportional to the electric field$$v(y)=\mu E(y)$$where $\mu$ is the mobility of carriers. For electrons in silicon$${\mu }_{e(b)}=1400{\text{cm}}^2{\text{V}}^{-1}{\text{s}}^{-1}$$It is the mobility when electrons are moving inside the bulk silicon
    • When electrons are moving near the silicon-oxide interface, the mobility is lower due to more scattering$${\mu }_{e(s)}=600{\text{cm}}^2{\text{V}}^{-1}{\text{s}}^{-1}$$
    • For holes in silicon
  • The current is given by$$I_{\text{D}}=C_{ox}W(V_{\text{G}}-V_{\text{T}}-V(y))\mu E(y)$$

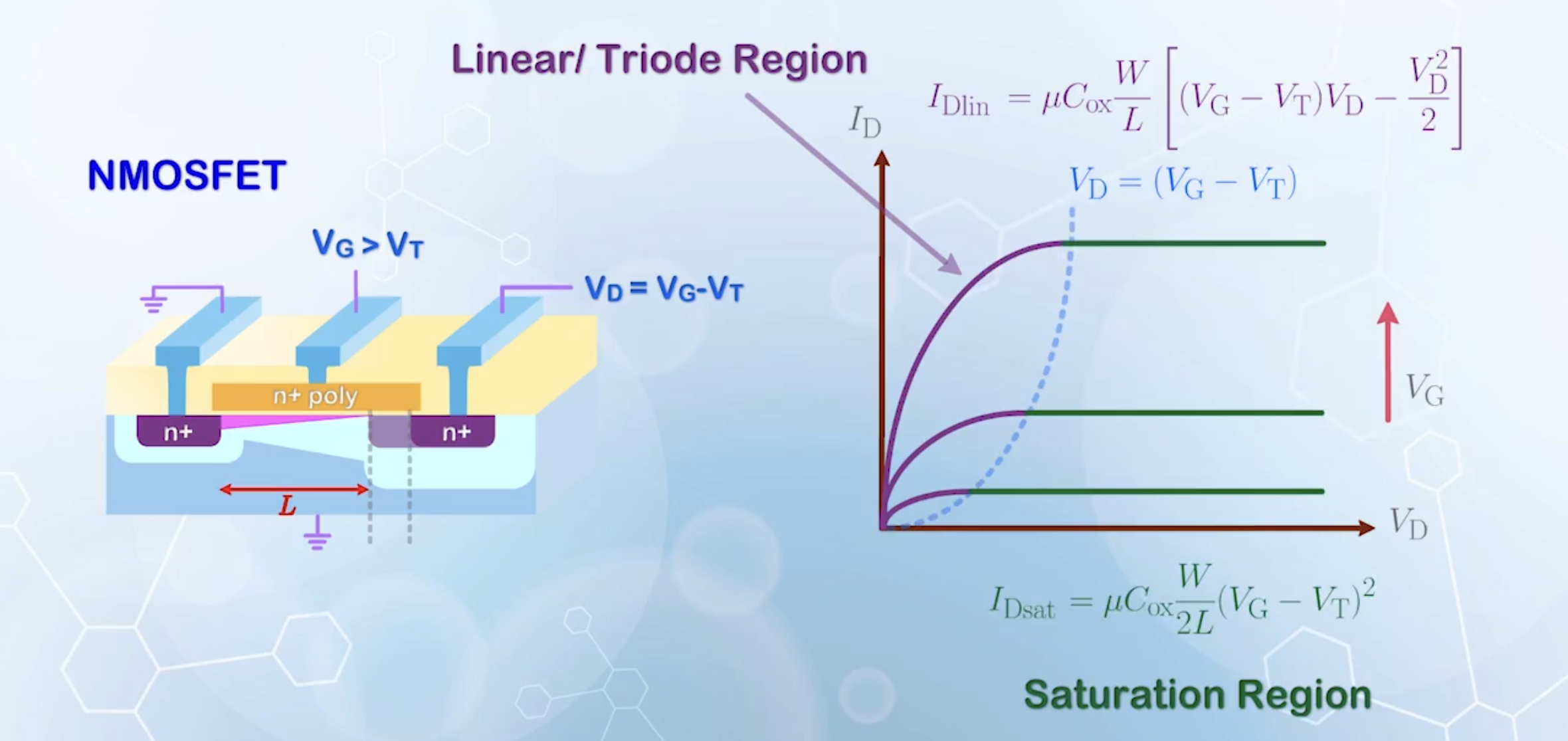
# Linear Region Current Equation

• The electric field is the negative gradient of voltage

  $$E(y)=\frac{\mathrm{d}V(y)}{\mathrm{d}y}$$

• Now the current equation becomes

  $$I_{\text{D}}\mathrm{d}y=C_{ox}W\mu (V_{\text{G}}-V_{\text{T}}-V(y))\mathrm{d}V(y)$$

  There should be a negative sign in the equation, but let’s focus on the magnitude for now

• Integrating both sides from source to drain

• A simpler approach is

  • The current is also given by$$I_{\text{D}}=Q_{\text{avg}}{v}_{\text{avg}}$$
  • The average charge per unit length is just the average of the charge at source and drain$$Q_{\text{avg}}=C_{ox}W(V_{\text{G}}-V_{\text{T}}-\frac{V_{\text{D}}}{2})$$
  • As of the average velocity$$v_{\text{avg}}=\mu E_{\text{avg}}$$
  • If we assume the electric field is uniform along the channel$$E_{\text{avg}}=\frac{V_{\text{D}}}{L}$$
  • In reality, the electric field near the source is lower, and that near the drain is higher, as electrons move faster near the drain
  • However, integrating $E$ over the channel length must give $V_{\text{D}}$ still, so the average electric field is still $V_{\text{D}}/L$
  • Therefore,$$I_{\text{D}}=C_{ox}W(V_{\text{G}}-V_{\text{T}}-\frac{V_{\text{D}}}{2})\mu \frac{V_{\text{D}}}{L}$$which is the same as the previous result

# Saturation Region Current Equation

As $V_{\text{D}}$ increases, $I_{\text{D}}$ will increase until $V_{\text{D}}=V_{\text{G}}-V_{\text{T}}$. If we still follow the previous current equation, when $V_{\text{D}}$ exceeds $V_{\text{G}}-V_{\text{T}}$, the current will start to decrease, and eventually become $0$. But from measurements, the current of a MOSFET eventually saturates and becomes a constant with a high enough $V_{\text{D}}$.

• For the inversion charge distribution

  $$C_{ox}W(V_{\text{G}}-V_{\text{T}}-V(y))$$

  to be valid, $V_{\text{G}}-V_{\text{T}}-V(y)$ must be positive. Otherwise, the channel will be depleted, and there will be no charge for conduction

  • This will happen at the drain when $V_{\text{D}}$ becomes larger than $V_{\text{G}}-V_{\text{T}}$

  • A pinchoff region, where the channel is depleted, will form near the drain

  • The channel can be separated into two different regions by the $V(y)=V_{\text{G}}-V_{\text{T}}$ point

    • Gradual channel region: the region where , inversion charge exists, and the channel behaves like a conductor
    • Pinchoff region: the region where , inversion charge is depleted, and the channel becomes an insulator

  • All drain voltage beyond $V_{\text{G}}-V_{\text{T}}$ will be dropped across the pinchoff region

  • !!!INCONSISTENCY MENTIONED!!!

    In the pinchoff region, the channel is depleted, and $Q(y)=0$. Meanwhile, the current is given by $I_{\text{D}}=Q(y)v(y)$. How can there be a current if there is no charge?

    This inconsistency will be resolved later, and for now, we just forget about the pinchoff region, and assume the drain is moved to the $V_{\text{G}}-V_{\text{T}}$ point, with $V_{\text{D}}$ picking up the value of $V_{\text{G}}-V_{\text{T}}$.

  • Assuming the pinchoff region is very small compared to the channel length, and the length of the gradual channel region can be approximated as $L$

  • Then, the current in the pinchoff condition is calculated with the same equation as before, but with $V_{\text{D}}$ replaced by $V_{\text{G}}-V_{\text{T}}$

    Any $V_{\text{D}}$ beyond $V_{\text{G}}-V_{\text{T}}$ will be dropped across the pinchoff region, and will not affect the current

• Therefore, the final current equation is

  • The first region is called the linear region or triode region, and the second region is called the (current) saturation region
  • The separation between the two regions is$$V_{\text{Dsat}}=V_{\text{G}}-V_{\text{T}}$$

  

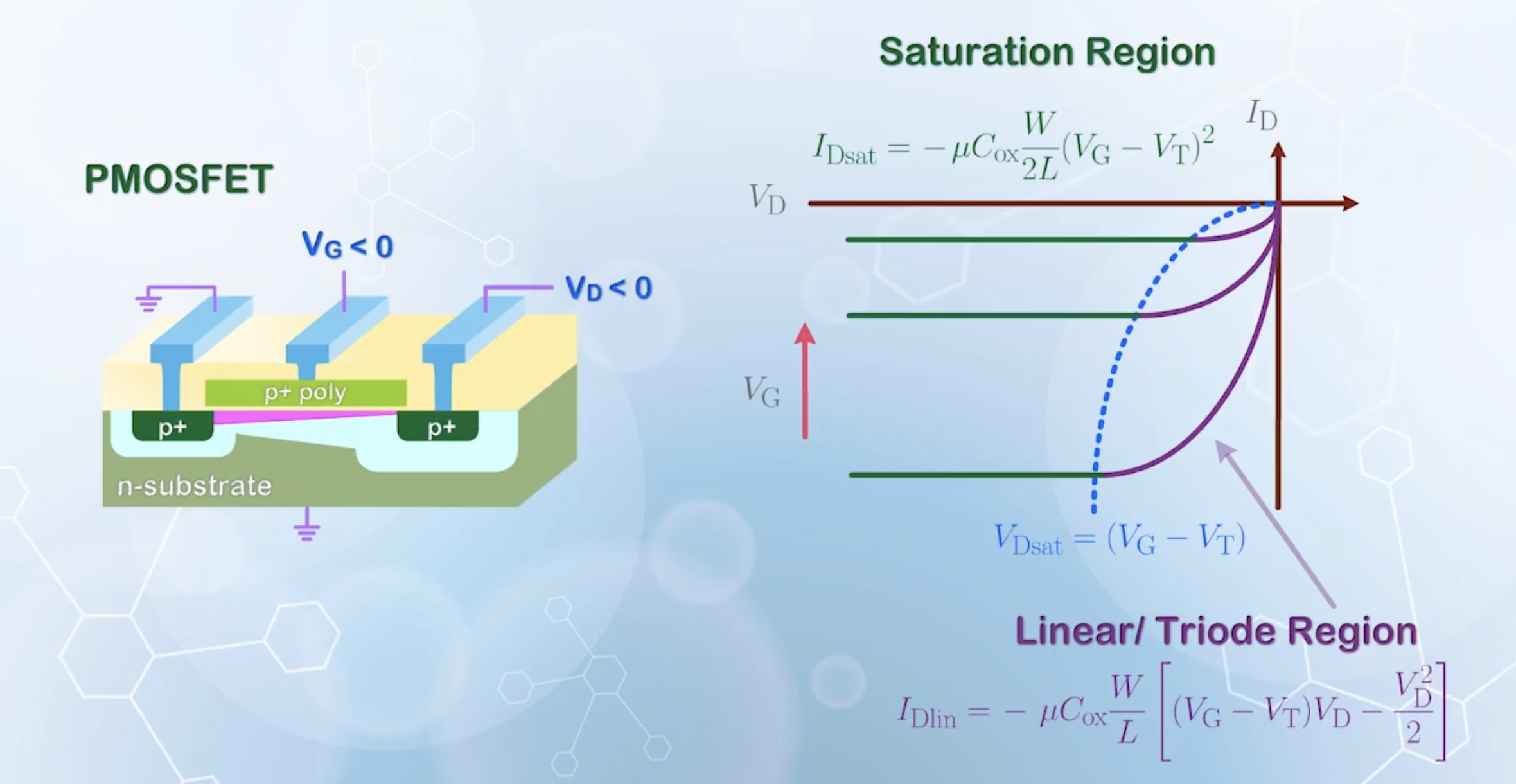
• Same applies to PMOSFET, with voltages and currents become negative relative to the source

  • Negative sign is added to the current, as the current in PMOSFET flows out of the drain

  

# Channel Length Modulation

Previously, we assumed the drain voltage beyond $V_{\text{Dsat}}$ does not affect $I_{\text{D}}$. However, in reality, increasing $V_{\text{D}}$ beyond $V_{\text{Dsat}}$ will extend the pinchoff region further into the channel, and the length of the gradual channel region will be reduced. As a result, $I_{\text{D}}$ will increase. This is the channel length modulation effect, describing how $V_{\text{D}}$ affects $I_{\text{D}}$ by changing the effective channel length.

• In saturation region, the current is given by$$I_{\text{Dsat}}=\frac{1}{2}\mu C_{ox}\frac{W}{L_{\text{ch}}}(V_{\text{G}}-V_{\text{T}}{)}^2$$where $L_{\text{ch}}$ is the length of the region where the channel voltage increases from $0$ to $V_{\text{Dsat}}$
• Replacing $L_{\text{ch}}$ with $L-\mathrm{\Delta }L$, and perform some mathematical magic, we have
• To calculate $\mathrm{\Delta }L$, we use Poisson’s equation
  • In the pinchoff region, there are only the depleted charge from the dopant ions
  • Therefore, the charge density is$$\rho =q{N}_A$$
  • Integrate twice to get the voltage difference across the pinchoff region$$V=\frac{q{N}_A}{2{\epsilon }_{\text{Si}}}(\mathrm{\Delta }L{)}^2$$
  • The voltage across the pinchoff region is $V_{\text{D}}-V_{\text{Dsat}}$
  • Thus,$$\mathrm{\Delta }L=\sqrt{\frac{2{\epsilon }_{\text{Si}}}{q{N}_A}(V_{\text{D}}-V_{\text{Dsat}})}$$
  • Putting it back$$I_{\text{Dsat}}=I_{\text{Dsat0}}(1+\frac{1}{L}\sqrt{\frac{2{\epsilon }_{\text{Si}}}{q{N}_A}(V_{\text{D}}-V_{\text{Dsat}})})$$

  • !!!INCONSISTENCY BACK AGAIN!!!

    For the same reason mentioned before, $\mathrm{\Delta }L$ given here is physically incorrect, as assuming the pinchoff region only contains depleted charge is physically incorrect.

• $I_{\text{Dsat}}$ has a square root dependence on $V_{\text{D}}$ beyond $V_{\text{Dsat}}$
• As the range of $V_{\text{D}}$ is limited, we can linearize the equation$$I_{\text{Dsat}}\approx I_{\text{Dsat0}}(1+\lambda V_{\text{D}})$$where $\lambda$ is the channel length modulation parameter
• The slope in the $I_{\text{D}}-V_{\text{D}}$ curve is then given by $I_{\text{Dsat}}\lambda$, and the output resistance is$$r_{\text{o}}=\frac{1}{\lambda I_{\text{Dsat0}}}$$which is similar to the output resistance of a BJT, which is given by$$r_{\text{o}}=\frac{V_A}{I_{\text{C}}}$$with $V_A$ replaced by $1/\lambda$ and $I_{\text{C}}$ replaced by $I_{\text{Dsat0}}$
  • Therefore, $1/\lambda$ is sometimes called the $V_A$ of a MOSFET, and the unified output resistance equation is$$r_{\text{o}}=\frac{V_A+V_{\text{D}}}{I_{\text{Dsat}}}\approx \frac{V_A}{I_{\text{Dsat}}}$$assuming $V_A\gg V_{\text{D}}$

# Inconsistencies in the Pinchoff Model

We have derived different equations for the MOSFET current in linear and saturation regions based on the pinchoff model.

• For $$I_{\text{Dlin}}=\mu C_{ox}\frac{W}{L}[(V_{\text{G}}-V_{\text{T}})V_{\text{D}}-\frac{V_{\text{D}}^2}{2}]$$
• For $$I_{\text{Dsat}}=\frac{1}{2}\mu C_{ox}\frac{W}{L}(V_{\text{G}}-V_{\text{T}}{)}^2(1+\lambda V_{\text{D}})$$
• There are some inconsistencies
  • Mathematical inconsistencies: using the two equations, the current at $V_{\text{D}}=V_{\text{G}}-V_{\text{T}}$ is not continuous
    • Actually, the equation given for the saturation region is only used to illustrate the effect of $V_{\text{D}}$ on $I_{\text{D}}$, and is never used to calculate $I_{\text{Dsat}}$ besides finding the slope after differentiation
    • The simplest way to correct for the discontinuity is just substitute $V_{\text{D}}$ with $V_{\text{D}}-V_{\text{Dsat}}$, but who cares?
    • We just assume the channel length modulation effect is very small, and use $I_{\text{Dsat0}}$ to approximate $I_{\text{Dsat}}$
  • Physical inconsistencies: according to the pinchoff model, $Q(y)=0$ for $y$ in the pinchoff region. To obtain a finite current, $v(y)$ must be infinite. However, based on the knowledge of relativity theory, the speed of light is the limit of all measurable speed, so the velocity of electrons cannot be infinite
• However, it is still a good approximation to reality in some special cases
• These are the limitations of the pinchoff model, more accurate models will be discussed later

文件历史